Table of contents:

• Introduction
• The story
• The problem
• Auto-vectorized code analysis
  • Step counter calculation
  • Null character detection
  • Performance effect of the step counter type
• Manual optimization of auto-vectorized code
• Benchmark results
  • Null-terminated input
  • Known size input
• Conclusion
• Future work
• Links

Code on GitHub

Introduction

In this post I will analyze a piece of C code automatically vectorized by GCC and improve its performance up to 1.9x by doing manual vectorization with using C++ and SIMD intrinsic functions:

This post hopefully will be useful for people who are interested in the topic of code vectorization and low level code optimization but experts in the topic can hardly find anything new in this post.

Note
I’m not a full time expert in the topic of code vectorization and low level code optimization but I occasionally spend time on this at my work. This post was a good opportunity for me to gain more knowledge on the subject.

I welcome any feedback on this post

For the sake of simplicity I will limit myself to x86-64 platform and AVX2 and earlier vector instructions. I will not touch AVX-512 because it is more complex and nuanced and also slightly less useful because many CPUs that are still in use (especially AMD ones) does not support AVX-512. All in all I’m leaving AVX-512 for another time.

Unless said otherwise all the assembly below is generated by compiling the source code on Compiler Explorer using x86-64 gcc 13.2 with flags -std=c++20 -O3 -ffast-math -Wall -DNDEBUG -march=x86-64-v3. x86-64-v3 means a “generic” x86-64 CPU with microarchitecture level 3 that has AVX2 but no AVX-512. Building for more specific architecture would indeed generate more optimized code but for our case of learning the generated code is essentially the same. Note that benchmarks were compiled for specific architecture.

To understand the code parts you will need a bit of a knowledge on C, C++ and assembler. There is a refresher (one more) for the latter.

If you only want to see the benchmark results then you can go directly to benchmark results.

The story

One day I’ve got disrupted by a post on Habr (a blog platform popular among Russian speaking IT community) which was a translation of a series of posts “{n} times faster than C” by Owen Shepherd. (ycombinator discussion).

The post was not particularly inspiring until user dllmain posted a comment where he’s offered a code that was more than 5 times faster than the best solution from the post itself (26.6 GiB/s vs ~4.5 GiB/s as per the comment) all because of unlocking the mighty power of C/C++ compilers to perform automatic vectorization. The comment got viral on Russian speaking C++ Twitter (or should I say X this days?), partially because of a heated discussion about undefined behavior in this code and caught my attention. From that this post was born.

The problem

Let’s take a look on what is the task that the post author was trying to optimize. It’s pretty simple: you need to count particular characters in a null-terminated string. For each character s the counter should be incremented and for each charater p decremented. The most naive solution looks like this:

int naive(const char *input) {
    int res = 0;
    while (true) {
        char c = *input++;
        switch (c) {
        case 0:
            return res;
        case 's':
            res++;
            break;
        case 'p':
            res--;
            break;
        default:
            break;
        }
    }
}

The much faster solution from dllmain is not so naive. I should also warn that it isn’t the most beautiful piece of C code you’ve ever seen so be prepared. Besides the arguable readability this code has two bugs (which dllmain had fixed in the follow up comments) and an undefined behavior (UB). Here is the code with my comments added:

#define step_size 128
#define auto __auto_type
#define proc(v) ({ auto _v = (v); (_v == 's') - (_v == 'p'); })
#define aligned(ptr, align) ({ \
    auto _ptr = (ptr); \
    auto _align = (align); \
    auto _r = (long long)_ptr & _align - 1; \
    _r ? _ptr + (_align - _r) : _ptr; \
})

int run_switches(const unsigned char* i) {
    auto r = 0;
    for (auto head_end = aligned(i, step_size); i != head_end && *i; ++i) r += proc(*i);
    // Bug 1: missed check for reaching the end of the string:
    // if (!*i) return r;
    while (1) {
        // Bug 2: `signed char` overflows on a string with 128 consequtive 's' characters.
        signed char step_r = 0;
        unsigned char rs[step_size];
        for (auto n = 0; n != sizeof(rs); ++n) {
            rs[n] = i[n] ? 0 : ~0;
            step_r += proc(i[n]);
        }
        long long* _ = rs;
        if (_[0] | _[1] | _[2] | _[3] | _[4] | _[5] | _[6] | _[7] | _[8] | _[9] | _[10] | _[11] | _[12] | _[13] | _[14] | _[15]) {
            while (*i) r += proc(*i++);
            break;
        }
        r += step_r;
        i += sizeof(rs);
    }
    return r;
}

The function has a UB because it reads its input in (aligned) 128 byte blocks and may read the data past the end of the input buffer. Despite it is a UB in C/C++ the operation itself is harmless on x86 platform (and possibly other platforms with paginated memory) as far as the read is not crossing the memory page boundary which is not happening in this code. Few glibc functions including strlen use the same approach to maximize performance (see AVX2 optimized strlen). Unlike the example code they’re written in assembler and hence escape from the C/C++ UB. Note that the address sanitizer still would not be happy about it.

Discussing UB is outside of this post scope. Let’s just assume that under some conditions it is a valid optimization approach on x86 platform to read past the end of an allocated buffer if the read is happening within the same memory page and concentrate on the performance aspect of the above code.

In this post I will explain what compiler has generated out of dllmain’s code, how it is so fast and will make it even faster with explicit use of SIMD instructions, particularly Intel’s AVX2.

Auto-vectorized code analysis

Let’s look at the dllmain’s code. It’s straightforward that compiler has vectorized it so it processes more than one input character in one step of the loop. That is what made this code to run 5-15 times faster than the fastest naive solution. What is interesting is what the generated code looks like and how it works.

Below is a version of the original code with bugs fixed (but UB is still there). I’ve changed it to process input in 64 byte blocks instead of 128 so step_r does not overflow and also renamed the function to autoVec_64_Orig. I’ve choosen to fix the step_r overflow by reducing the step size from 128 to 64 bytes instead of using short for step_r because benchmarking showed that the second solution is ~10-90% slower. I’ll explain this later.

#define step_size 64

#define proc(v) ({ auto _v = (v); (_v == 's') - (_v == 'p'); })

#define aligned(ptr, align) ({ \
    auto _ptr = (ptr); \
    auto _align = (align); \
    auto _r = (long long)_ptr & (_align - 1); \
    _r ? _ptr + (_align - _r) : _ptr; \
})

int autoVec_64_Orig(const unsigned char* i) {
    auto r = 0;
    for (auto head_end = aligned(i, step_size); i != head_end && *i; ++i) {
        r += proc(*i);
    }
    if (!*i) {
        return r;
    }
    while (1) {
        signed char step_r = 0;
        unsigned char rs[step_size];
        for (auto n = 0; n != sizeof(rs); ++n) {
            rs[n] = i[n] ? 0 : ~0;
            step_r += proc(i[n]);
        }
        auto _ = reinterpret_cast<const long long*>(rs);
        if (_[0] | _[1] | _[2] | _[3] | _[4] | _[5] | _[6] | _[7]) {
            while (*i) r += proc(*i++);
            break;
        }
        r += step_r;
        i += sizeof(rs);
    }
    return r;
}

Compiler Explorer

If you want, you can compare it with assembly of naiveTableInt - the fastest naive soultion that uses table to avoid branching.

The function consists of three parts: the first part is a naive non vectorized loop where the input is processed 1 character per step, the second and the main part is a vectorized loop where the input is processed in 64 character blocks per step which allows vectorization and the last part is again a naive non vectorized loop where the input is processed 1 character per step.

The whole purpose of the first loop is to get to the aligned position in input before starting the vectorized, otherwise reading in 64 byte blocks may cross the memory page boundary and hit a non allocated page which will cause a segfault and the program termination.

The first and the last parts of the function are nothing special so we will only look into the auto-vectorized main part. Let’s see what magic the compiler did for us there.

Below is the assembly of the main loop of autoVec_64_Orig. I’ve reordered some operations to keep logically related parts together and removed few unrelated bits.

        ; Start of the main loop
        ; Set all 256 bits of ymm4 and ymm5 registers to zero
        vpxor   xmm4, xmm4, xmm4
        vpxor   xmm5, xmm5, xmm5

        ; Set all 32 8-bit integers of ymm3 register to 'p'
        mov     edx, 112
        vmovd   xmm3, edx
        vpbroadcastb    ymm3, xmm3

        ; Set all 32 8-bit integers of ymm2 register to 's'
        mov     edx, 115
        vmovd   xmm2, edx
        vpbroadcastb    ymm2, xmm2

        ; Jump to the loop body
        jmp     .L9

.L6:    ; Advance to the next step
        movsx   r8d, r8b                    ; Sign-extend step counter `step_r` from byte to int
        add     esi, r8d                    ; Add it to the total counter (`r`)
        add     rax, 64                     ; Increment input pointer by 64

.L9:
        ; Load 64 bytes of input from the memory into two 32-byte registers
        vmovdqu ymm7, YMMWORD PTR [rax]
        vmovdqu ymm0, YMMWORD PTR [rax+32]


        ; Calculate step counter (`step_r`) start with
        ; calculating it for each input byte separately
        vpcmpeqb        ymm1, ymm7, ymm3    ; Compare each byte of the first input register with 'p'
        vpcmpeqb        ymm7, ymm7, ymm2    ; Compare each byte of the first input register with 's'
        vpsubb  ymm1, ymm1, ymm7            ; Subtract one from another (32 subtracts of 8-bit integers)

        vpcmpeqb        ymm7, ymm0, ymm3    ; Compare each byte of the second input register with 'p'
        vpaddb  ymm1, ymm1, ymm7            ; Add to the step counter (32 additions of 8-bit integers)

        vpcmpeqb        ymm0, ymm0, ymm2    ; Compare each byte of the second input register with 's'
        vpsubb  ymm1, ymm1, ymm0            ; Subtract from the step counter (32 subtracts of 8-bit integers)

        ; Sum up 32 8-bit step counters to one `step_r`
        vextracti128    xmm0, ymm1, 0x1     ; Sum up four 64-bit elements of `step_r`
        vpaddb  xmm0, xmm0, xmm1            ;
        vpsrldq xmm1, xmm0, 8               ;
        vpaddb  xmm0, xmm0, xmm1            ;
        vpsadbw xmm0, xmm0, xmm5            ; Horizontally sum each consequitive 8 absolute differences, check notes below
        vpextrb r8d, xmm0, 0                ; Take the lowest byte of the result

        ; Check input for null characters
        vpcmpeqb        ymm1, ymm7, ymm4    ; Compare each byte of the first input register with zero
        vpcmpeqb        ymm8, ymm0, ymm4    ; Compare each byte of the second input register with zero
        vpor    ymm6, ymm1, ymm8            ; Bitwise OR two 32-byte parts

        ; Bitwise OR 4 64-bit integers to get a single 64-bit integer
        vextracti128    xmm1, ymm6, 0x1     ; 
        vpextrq rcx, xmm1, 1                ;
        vpsrldq xmm0, xmm6, 8               ;
        vpor    xmm0, xmm0, xmm6            ;
        vpor    xmm0, xmm0, xmm1            ;
        vmovq   rdx, xmm0                   ;
        or      rdx, rcx                    ; Final OR to set the flag. Flag is set if any of the input bytes contains the null character
        je      .L6                         ; If zero null characters found jump to the next step of the loop

        ; Else proceed to the next part

vpsadbw instruction

vpsadbw horizontally sums each consequitive 8 absolute differences (here it is |counters[i] - nulls[i]|) and puts results into N 16-bit integers. This is the way to sum all 8-bit unsigned integers (in groups of 8) in 16/32/64-byte register with a single instruction.

For 16-byte register (xmm, AVX) it produces two, for 32-byte register (ymm, AVX2) - four and for 64-byte register (zmm, AVX-512) - eight 16-bit results.

I have visualized the blocks of generated code so you can understand it without digging into assembler. For simplicity I’ve drawn operating on 16-byte registers instead of 32-byte registers.

Before starting the main loop, the program sets each byte of (32-byte register) ymm3 to p, each byte of ymm2 to s and each byte of ymm4 and ymm5 to zero. That’s to perform comparisons and other vector operations later. On each loop on the main cycle, the program loads the input from memory into registers (two 32 byte input registers ymm7 and ymm0 for our case). Then it calculates step counter step_r and detects the null character presense in the input.

Step counter calculation

The program calculates per character counters by comparing each byte in input registers with 'p' and 's'. Each comparison is done by a single instruction vpcmpeqb which compares the operands byte by byte, then the results of comparisons substituted from each other byte by byte (vpsubb):

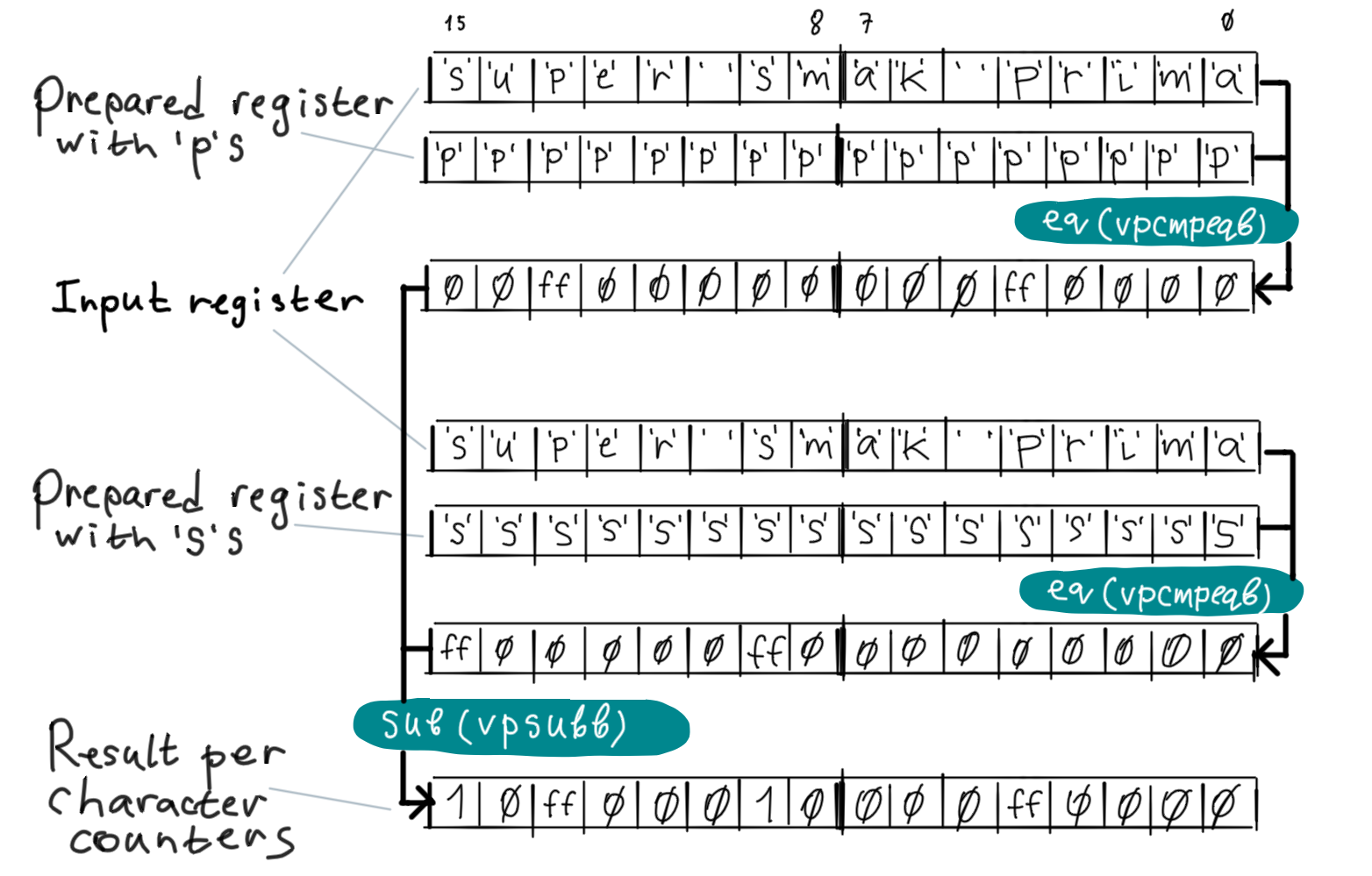
Note that the result of vpcmpeqb is 0xFF if bytes are equal, 0 otherwise. 0xFF is -1 when treated as signed 8-bit integer which means that the character counters are initially negated so we need to revese the order of operands for subtraction.

Also note that all registers are shown in reverse byte order, so the real input is "amirp kams repus".

In our code we have two input registers so after comparing and subtracting counters for the first input register, the program will do the same for the second one.

After the program has calculated per character counters for the whole input it “devectorizes” (or “folds”) it into a scalar counter to add it to the result counter r. It does it in two steps, first it adds up 8-byte parts into the lowest 8-byte part of the register. The addition is done by vpaddb which adds inputs byte by byte.

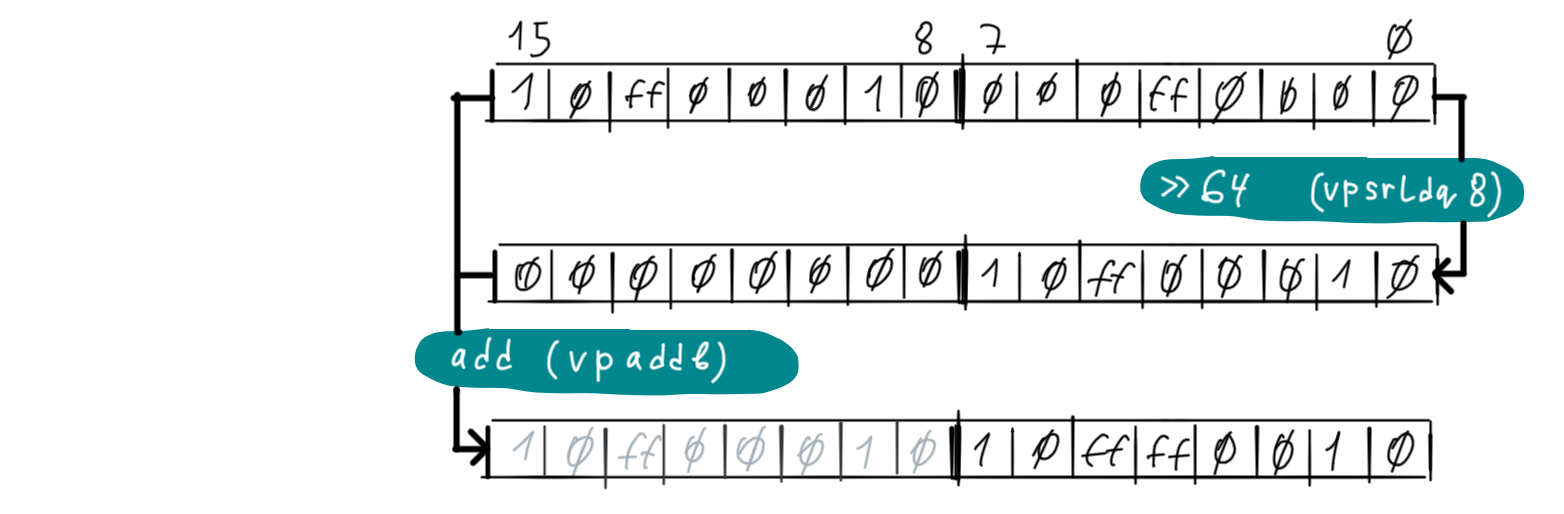
In our code we first add the high 16-byte half of the counters register to the lower one with using vextracti128 and vpaddb and then do the 8 byte shift shown on the above picture.

Now the program has all the per character counters accumulated in the lowest 8 bytes of the register and it can do a so called horizontal operation: sum up all this 8 counters together. There is no instruction to do exactly this so the program uses vpsadbv described above:

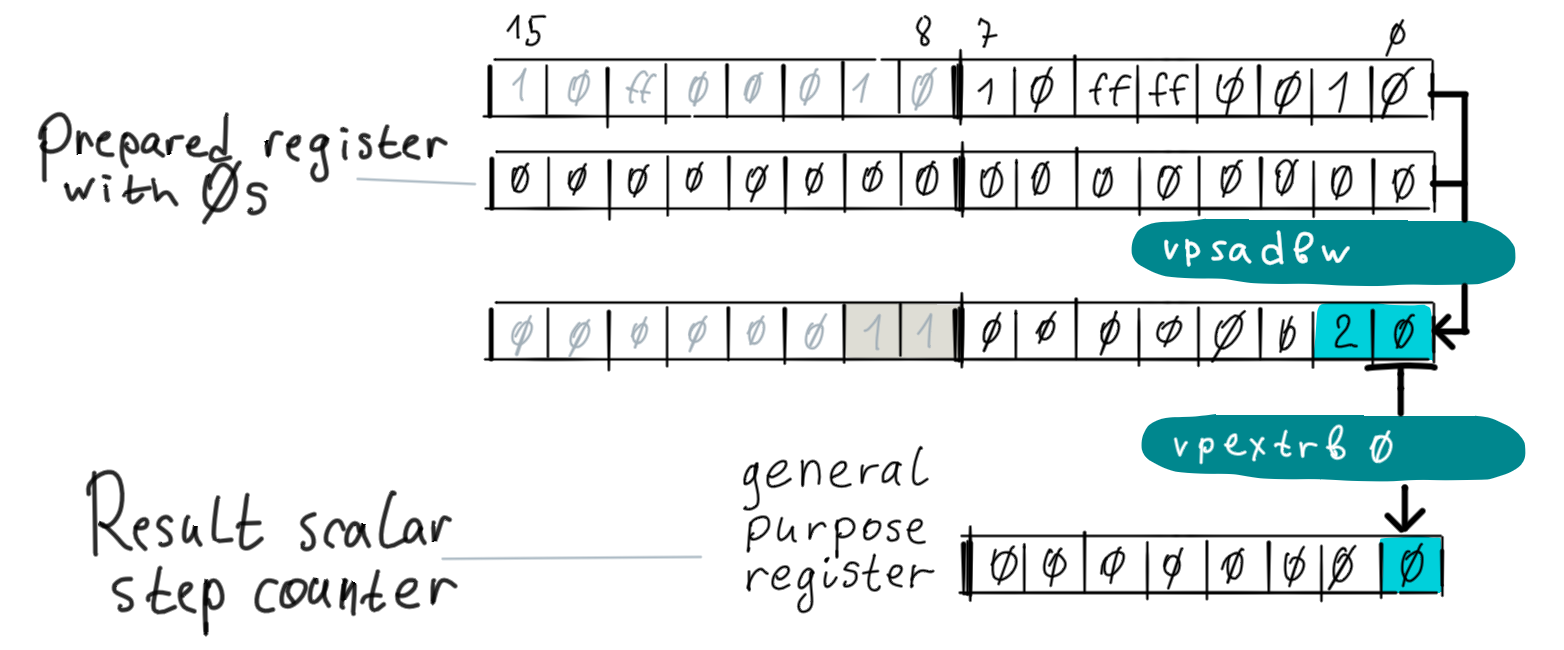
After this the program extracts the result’s lowest byte to a general purpose register it treats it as a signed char. The extracted number represents the step counter step_r. At the end of each cycle the program adds it to the result counter r.

Null character detection

Presense of the null character is detected in a way similar to counting characters. First, the input registers are compared byte by byte with precreated vector of zeroes:

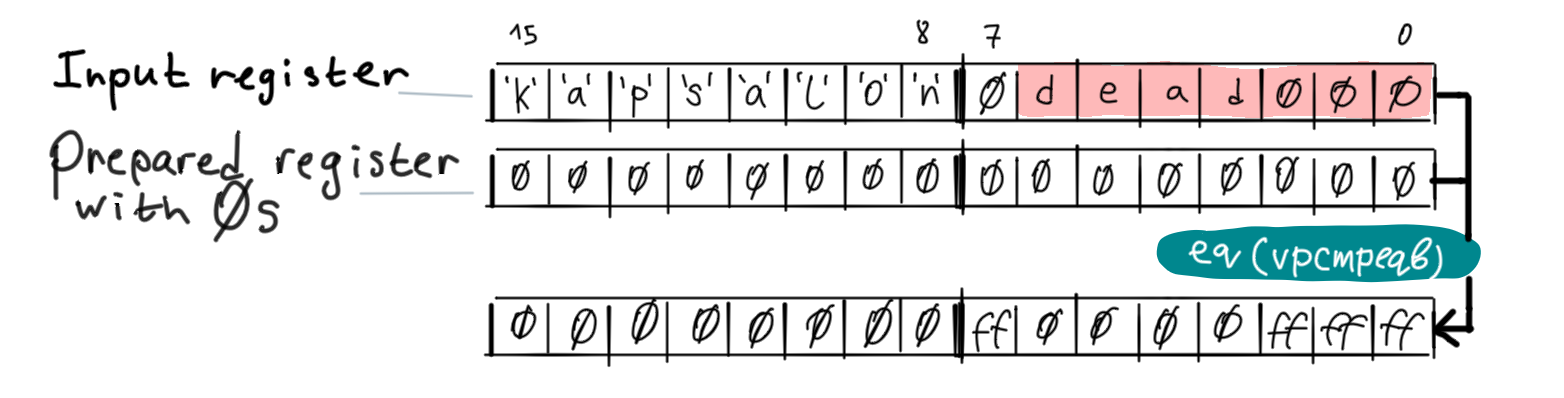
In our code we have two input registers so after comparing the first input register with zeroes, the program will do the same for the second one then it will bitwise OR both results with using vpor instruction.

Once per character “null” flags are calculated in a vector register the program devectorizes it into a general purpose register so it can do a conditional jump on it (any non-zero bit means that there is the null character so the program must break from the vectorized loop). There are several ways of doing it but they’re all more or less about bitwise OR-ing (with vpor) all 8-byte parts of the register together and then moving it to a general purpose register:

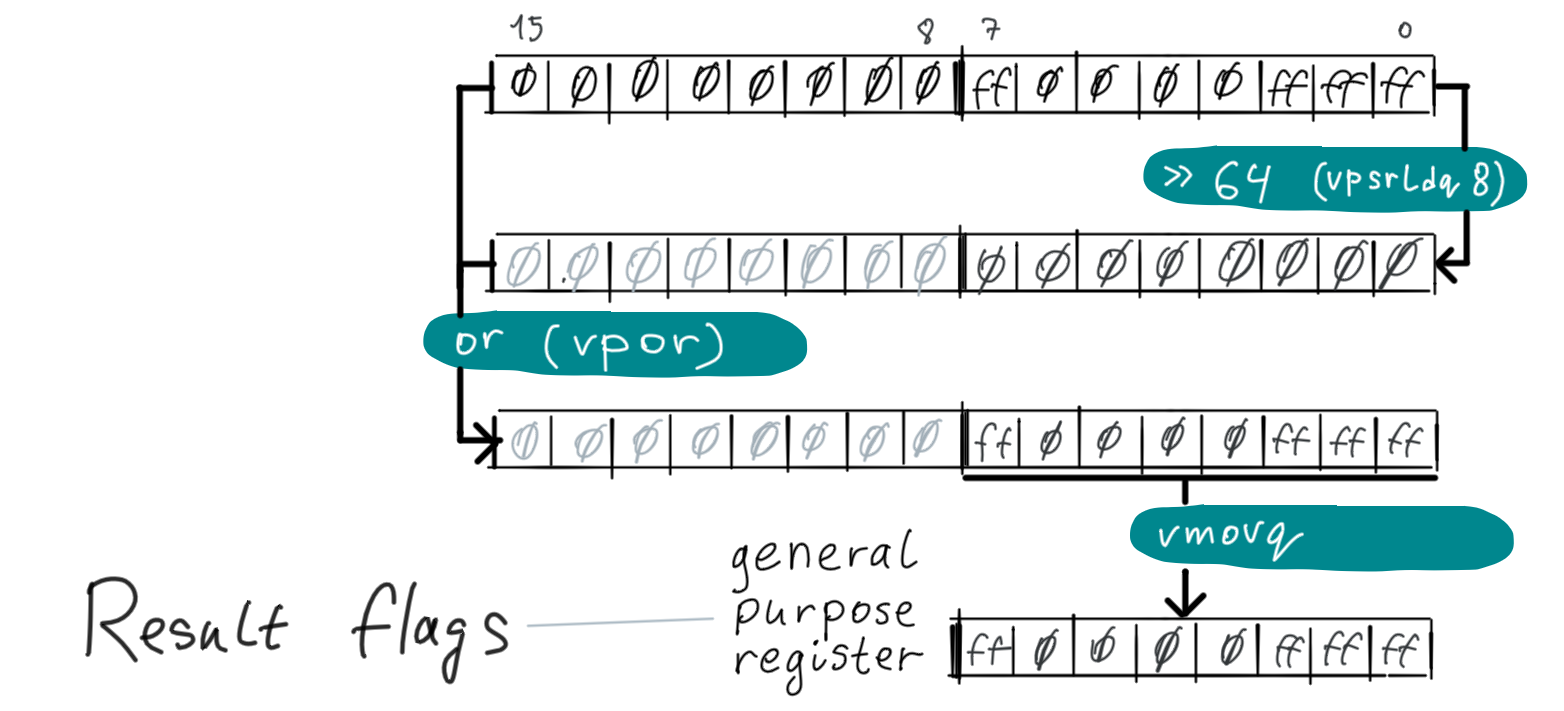
In our code we also bitwise OR the high 16-byte half of the per character “null” flags register to the lower half with using vextracti128 and vpor.

In our code the devectorization for the null character detection looks more complex, e.g. it moves parts of the vector register to a general purpose register twice (High 8 bytes with vpextrq rcx, xmm1, 1 then low 8 bytes with vmovq rdx, xmm0) and then bitwise OR them. I have not researched why it is like that, probably compiler thinks that it performs faster than more trivial code but I can’t see this in the benchmark results.

Performance effect of the step counter type

So why changing the step counter (step_r) type from signed char to short degrades performance that much? Because only if the type is signed char the compiler can use vpsadbw to sum per character counters and ignore possible overflow for the reason that the lowest byte of the result is still correct.

If the step counter type is not signed char then compiler generates code that sums up per character counters in less effective way with a lot of vpmovzxbw, vpsrldq and vpaddw instructions.

Manual optimization of auto-vectorized code

Now let’s try to make the above code faster. For this I will do manual vectorization by using Intel specific intrinsics functions. As I said earlier, I will only use AVX2 and earlier vector instructions here.

Before doing optimization I’ve rewritten autoVec_64_Orig with manually vectorized code. (I’ve barely used auto to make it easier to understand) :

#include <cstdint>
#include <cstddef>
#include <immintrin.h>

template <std::size_t Alignment>
inline __attribute__((always_inline)) const char* alignedAfter(const char* ptr) noexcept {
    auto offset = reinterpret_cast<std::uintptr_t>(ptr) & (Alignment - 1);
    return offset ? (ptr + Alignment - offset) : ptr;
}

constexpr __attribute__((always_inline)) int charValue(char c) noexcept {
    return (c == 's') - (c == 'p');
}

int manualVec_64_Orig(const char* input, std::size_t) noexcept {
    constexpr std::size_t StepSize = 64;

    int res = 0;

    // Process unaligned preamble in naive way
    for (const auto headEnd = alignedAfter<StepSize>(input); input != headEnd && *input; ++input) {
        res += charValue(*input);
    }
    if (!*input) [[unlikely]] {
        return res;
    }

    const __m256i nulls = _mm256_set1_epi8(0); // Fill all 32 8-bit integers with 0
    const __m256i ps = _mm256_set1_epi8('p'); // Fill all 32 8-bit integers with 'p'
    const __m256i ss = _mm256_set1_epi8('s'); // Fill all 32 8-bit integers with 's'

    while (true) {
        // We use aligned load because we know that the input is aligned
        const __m256i block0 = _mm256_load_si256(reinterpret_cast<const __m256i*>(input));
        const __m256i block1 = _mm256_load_si256(reinterpret_cast<const __m256i*>(input + sizeof(__m256i)));

        __m256i eqNull = _mm256_cmpeq_epi8(nulls, block0);
        eqNull = _mm256_cmpeq_epi8(eqNull, block1);

        __m256i counters = _mm256_sub_epi8(_mm256_cmpeq_epi8(ps, block0), _mm256_cmpeq_epi8(ss, block0));
        counters = _mm256_add_epi8(counters, _mm256_cmpeq_epi8(ps, block1));
        counters = _mm256_sub_epi8(counters, _mm256_cmpeq_epi8(ss, block1));

        // Horizontally sum each consequitive 8 absolute differences (abs(counters[i] - nulls[i])) and put results into four 16-bit integers
        // that is an intrinsic for `vpsadbw` instruction that I've mentioned in the above `autoVec_64_Orig` assembly comments
        counters = _mm256_sad_epu8(counters, nulls);

        // Partially devectorize `counters`: sum four 64-bit integers of `counters` into the lowest 64-bit integer of `stepRes` (`stepRes[0]`)
        __m128i stepRes = _mm_add_epi64(_mm256_extracti128_si256(counters, 1), *reinterpret_cast<const __m128i*>(&counters));
        stepRes = _mm_add_epi64(_mm_bsrli_si128(stepRes, 8), stepRes);

        // Devectorize `eqNull`: bitwise or 4 64-bit integers of `eqNull` into one
        __m128i stepNull = _mm_or_si128(_mm256_extracti128_si256(eqNull, 1), *reinterpret_cast<const __m128i*>(&eqNull));
        stepNull = _mm_or_si128(_mm_bsrli_si128(stepNull, 8), stepNull);
        const long long anyNull = _mm_extract_epi64(stepNull, 0);
        if (anyNull) [[unlikely]] {
            // Found null character, calculate the remaining values char by char until we hit the null character
            while (*input) {
                res += charValue(*input++);
            }
            return res;
        }

        // Take the lowest byte of the 64-bit integer `stepRes[0]` and convert it to a signed char
        res += static_cast<signed char>(stepRes[0]);
        input += StepSize;
    }
}

Compiler Explorer

I will not change the overall algorithm because it looks reasonable to me but I will improve slow parts. To get a grasp on how slow particular instructions are I use a latency table. Also most latencies are listed on Intel Intrinsics Guide - a resource you can’t avoid if you’re programming with Intel intrinsics.

As you can see from the assembly, the essential parts of the algorithm i.e. loading data, vector-comparing it with ‘p’, ‘s’ and 0 and also calculating per-character step counter takes only a small part of the overall code. Most of the code is about “devectorizing” or “folding” a vector of values to a single number, both for the null character check and for updating the result counter res. Сoincidentally this supplementary code is also slow because it uses high latency instructions like vextracti128 (latency is 3 on Intel CPUs), vpextrq (latency is 3 to 4), vpextrb (same). That’re quite high latencies taking into account that simple vector operations like comparison, logical operations and arithmetic all have a latency of 1. So CPU can either compare 3 * 32 = 96 characters with 0 or extract a half of xmm register to another register. All instructions that extract parts of a vector register are relatively slow. That’s a simplification of course: the CPU is more complex and instruction latency despite being important element is just one of many factors that affect performance, but you get the point.

We want to increase a number of times we do an essential algorithm parts operating on vectorized registers before we convert our vector results to scalar results in general purpose registers. The simplest solution would be to process more input characters per step, unfortunately we can’t just increase the step size because we’ve already reached the limit of how many characters we can count per step without overflowing our 8-bit step counter.

Remember that vpsadbw instruction (_mm256_sad_epu8 intrinsic)) sums up absolute values of 8-bit integers (so effectively it sums up unsigned ) and produces 16-bit result but we can only use the low 8-bit of it because we have signed 8-bit integers as the input (thus the high 8-bit of the vpsadbw result are incorrect). To be able to use all 16-bit of vpsadbw result we need to make its input positive. We can do this by incrementing each 8-bit integer by the number of steps:

    // Offset to add to counters to make them non-negative
    const __m256i vecOffset = _mm256_set1_epi8(BlocksPerStep); // Fill all 32 8-bit integers with `BlocksPerStep`
    constexpr int scalarOffset = BlocksPerStep * sizeof(__m256i);

    while (true) {
        ...
        // Offset 8-bit counters to make them non-negative
        counters = _mm256_add_epi8(counters, vecOffset);
        // Horizontally sum each consequitive 8 absolute differences (abs(counters[i] - nulls[i])) and put results into four 16-bit integers
        counters = _mm256_sad_epu8(counters, nulls);

        // Partially devectorize `counters`: sum four 64-bit integers of `counters` into one at `stepRes[0]`
        __m128i stepRes = _mm_add_epi64(_mm256_extracti128_si256(counters, 1), *reinterpret_cast<const __m128i*>(&counters));
        stepRes = _mm_add_epi64(_mm_bsrli_si128(stepRes, 8), stepRes);
        ...
        // Use the whole 64-bit `stepRes[0]` and compensate for the previously added offset
        res += (static_cast<int>(stepRes[0]) - scalarOffset);
        ...
    }

Now we can implement manualVec in a way that it can have step size bigger than 64. Note that BlocksPerStep must be less than 128 otherwise per-character counters may overflow hence step size must be less than 4096:

#include <cstdint>
#include <cstddef>
#include <type_traits>
#include <utility>
#include <immintrin.h>

template <std::size_t Alignment>
inline __attribute__((always_inline)) const char* alignedAfter(const char* ptr) noexcept {
    auto offset = reinterpret_cast<std::uintptr_t>(ptr) & (Alignment - 1);
    return offset ? (ptr + Alignment - offset) : ptr;
}

constexpr __attribute__((always_inline)) int charValue(char c) noexcept {
    return (c == 's') - (c == 'p');
}

template <std::size_t V>
using IndexConstant = std::integral_constant<std::size_t, V>;

namespace detail {
    template <class F, std::size_t... I>
    constexpr __attribute__((always_inline)) void repeatBlock(std::index_sequence<I...>, F&& f) {
        (f(IndexConstant<I>{}), ...);
    }
}

// Call `f` `N` times as `(f(IndexConstant<0>{}), f(IndexConstant<1>{}), ... f(IndexConstant<N-1>{}))`
template <std::size_t N, class F>
constexpr __attribute__((always_inline)) void forEach(F&& f) {
    detail::repeatBlock(std::make_index_sequence<N>{}, std::forward<F>(f));
}

constexpr int32_t PageSize = 4096;

template <std::size_t StepSize>
requires((StepSize <= PageSize)
    && (PageSize % StepSize == 0)
    && (StepSize % sizeof(long long) == 0))
inline int manualVec_A(const char* input) noexcept {
    constexpr std::size_t BlocksPerStep = StepSize / sizeof(__m256i);

    int res = 0;

    // Process unaligned preamble in naive way
    for (const auto headEnd = alignedAfter<StepSize>(input); input != headEnd && *input; ++input) {
        res += charValue(*input);
    }
    if (!*input) [[unlikely]] {
        return res;
    }

    const __m256i nulls = _mm256_set1_epi8(0); // Fill all 32 8-bit integers with 0
    const __m256i ps = _mm256_set1_epi8('p'); // Fill all 32 8-bit integers with 'p'
    const __m256i ss = _mm256_set1_epi8('s'); // Fill all 32 8-bit integers with 's'

    // Offset to add to counters to make them non-negative
    const __m256i vecOffset = _mm256_set1_epi8(BlocksPerStep); // Fill all 32 8-bit integers with `BlocksPerStep`
    constexpr int scalarOffset = BlocksPerStep * sizeof(__m256i);

    while (true) {
        __m256i eqNull;
        __m256i counters;
        forEach<BlocksPerStep>([&]<std::size_t Idx>(IndexConstant<Idx>) {
            // We use aligned load because we know that the input is aligned
            const __m256i block = _mm256_load_si256(reinterpret_cast<const __m256i*>(input) + Idx);

            if constexpr (Idx == 0) {
                eqNull = _mm256_cmpeq_epi8(nulls, block);
                counters = _mm256_sub_epi8(_mm256_cmpeq_epi8(ps, block), _mm256_cmpeq_epi8(ss, block));
            } else {
                eqNull = _mm256_or_si256(eqNull, _mm256_cmpeq_epi8(nulls, block));
                counters = _mm256_add_epi8(counters, _mm256_cmpeq_epi8(ps, block));
                counters = _mm256_sub_epi8(counters, _mm256_cmpeq_epi8(ss, block));
            }
        });

        // Each 8-bit counter in `counters` fits into signed char, effectively works for BlocksPerStep < 128 hence StepSize must be < 4096
        static_assert(BlocksPerStep < 128);

        // Offset 8-bit counters to make them non-negative
        counters = _mm256_add_epi8(counters, vecOffset);
        // Horizontally sum each consequitive 8 absolute differences (abs(counters[i] - nulls[i])) and put results into four 16-bit integers
        counters = _mm256_sad_epu8(counters, nulls);

        // Partially devectorize `counters`: sum four 64-bit integers of `counters` into the lowest 64-bit integer of `stepRes` (`stepRes[0]`)
        __m128i stepRes = _mm_add_epi64(_mm256_extracti128_si256(counters, 1), *reinterpret_cast<const __m128i*>(&counters));
        stepRes = _mm_add_epi64(_mm_bsrli_si128(stepRes, 8), stepRes);

        // Devectorize `eqNull`: bitwise or 4 64-bit integers of `eqNull` into one
        __m128i stepNull = _mm_or_si128(_mm256_extracti128_si256(eqNull, 1), *reinterpret_cast<const __m128i*>(&eqNull));
        stepNull = _mm_or_si128(_mm_bsrli_si128(stepNull, 8), stepNull);
        const long long anyNull = _mm_extract_epi64(stepNull, 0);
        if (anyNull) [[unlikely]] {
            // Found null character, calculate the remaining values char by char until we hit the null character
            while (*input) {
                res += charValue(*input++);
            }
            return res;
        }

        // Use the whole 64-bit integer and compensate for the added offset
        res += (static_cast<int>(stepRes[0]) - scalarOffset);

        input += StepSize;
    }
}

Compiler Explorer

manualVec_A can be called as manualVec_A<64>(input), manualVec_A<128>(input) etc.

So far so good: now we can do less devectorizations per input character by increasing the step size. Note that our change have not increased performance for 64 and less step sizes. It is even slightly decreased because we need to add and subtract the offset on each step.

We can do one more change in the same direction: introduce vector step counter resVec and devectorize it once once before break from the main loop:

template <std::size_t StepSize>
requires((StepSize <= PageSize)
    && (PageSize % StepSize == 0)
    && (StepSize % sizeof(long long) == 0))
inline int manualVec(const char* input) noexcept {
    constexpr std::size_t BlocksPerStep = StepSize / sizeof(__m256i);

    int res = 0;

    // Process unaligned preamble in naive way
    for (const auto headEnd = alignedAfter<StepSize>(input); input != headEnd && *input; ++input) {
        res += charValue(*input);
    }
    if (!*input) [[unlikely]] {
        return res;
    }

    const __m256i nulls = _mm256_set1_epi8(0); // Fill all 32 8-bit integers with 0
    const __m256i ps = _mm256_set1_epi8('p'); // Fill all 32 8-bit integers with 'p'
    const __m256i ss = _mm256_set1_epi8('s'); // Fill all 32 8-bit integers with 's'

    // Offset to add to counters to make them non-negative
    const __m256i vecOffset = _mm256_set1_epi8(BlocksPerStep); // Fill all 32 8-bit integers with `BlocksPerStep`
    constexpr int scalarOffset = BlocksPerStep * sizeof(__m256i);

    // Here we will accumulate vector step counters
    __m256i resVec{};

    while (true) {
        __m256i eqNull;
        __m256i counters;
        forEach<BlocksPerStep>([&]<std::size_t Idx>(IndexConstant<Idx>) {
            // We use aligned load because we know that the input is aligned
            const __m256i block = _mm256_load_si256(reinterpret_cast<const __m256i*>(input) + Idx);

            if constexpr (Idx == 0) {
                eqNull = _mm256_cmpeq_epi8(nulls, block);
                counters = _mm256_sub_epi8(_mm256_cmpeq_epi8(ps, block), _mm256_cmpeq_epi8(ss, block));
            } else {
                eqNull = _mm256_or_si256(eqNull, _mm256_cmpeq_epi8(nulls, block));
                counters = _mm256_add_epi8(counters, _mm256_cmpeq_epi8(ps, block));
                counters = _mm256_sub_epi8(counters, _mm256_cmpeq_epi8(ss, block));
            }
        });

        // Each 8-bit counter in `counters` fits into signed char, effectively works for BlocksPerStep < 128 hence StepSize must be < 4096
        static_assert(BlocksPerStep < 128);

        // Offset 8-bit counters to make them non-negative
        counters = _mm256_add_epi8(counters, vecOffset);
        // Horizontally sum each consequitive 8 absolute differences (abs(counters[i] - nulls[i])) and put results into four 16-bit integers
        counters = _mm256_sad_epu8(counters, nulls);

        // Devectorize `eqNull`: bitwise or 4 64-bit integers of `eqNull` into one
        __m128i stepNull = _mm_or_si128(_mm256_extracti128_si256(eqNull, 1), *reinterpret_cast<const __m128i*>(&eqNull));
        stepNull = _mm_or_si128(_mm_bsrli_si128(stepNull, 8), stepNull);
        const long long anyNull = _mm_extract_epi64(stepNull, 0);
        if (anyNull) [[unlikely]] {
            // Found null character, calculate the remaining values char by char until we hit the null character
            while (*input) {
                res += charValue(*input++);
            }

            // Devectorize `resVec`: fold 4 64-bit counters in resVec to a 64-bit integer with addition
            __m128i stepRes = _mm_add_epi64(_mm256_extracti128_si256(resVec, 1), *reinterpret_cast<const __m128i*>(&resVec));
            stepRes = _mm_add_epi64(_mm_bsrli_si128(stepRes, 8), stepRes);
            res += static_cast<int>(_mm_extract_epi64(stepRes, 0));
            return res;
        }

        // Accumulate counters in resVec
        resVec = _mm256_add_epi64(resVec, counters);

        // Compensate for added vecOffset
        res -= scalarOffset;

        input += StepSize;
    }
}

Compiler Explorer

I’ve benchmarked manualVec for different step size and found that it wins over original auto-vectorized version by almost a factor of two and decided to stop there. I’m pretty sure that it can be optimized even further with doing in-depth profiling and/or using AVX-512 instructions but that’s an exercise for another time or person.

Please check the next section for graphs and other benchmark results.

Benchmark results

I’ve tested performance of different solutions for the problem, both naive and vectorized.

The following solutions were benchmarked:

• algoHabrNaive - original, the most naive implementation from the original post
• algoHabrLessBranches - implementation from the original postthat uses conditional move instead of branching
• algoHabrTableChar - implementation from the original post that uses a table with signed char values (-1, 0, 1)
• algoHabrTableInt - implementation from the original post that uses a table with int values (-1, 0, 1)
• autoVec_64_Orig - original auto-vectorized implementation from dllmain with bugs fixed (step size is 64)
• autoVec_<StepSize> - generalized version of autoVec_64_Orig. It uses signed char for step counter for step sizes 32 and 64, short otherwise
• autoVec_128_WithOverflow - modification of autoVec_128 that uses signed char for step counter hence has the overflow bug
• autoVec_<StepSize>_IntStepCounter - modification of autoVec_<StepSize> that uses int for step counter
• manualVec_64_Orig - original non-optimized manually vectorized implementation
• manualVec_<StepSize> - optimized and generalized manually vectorized implementation
• manualVecSize_<StepSize> - version of manualVec_<StepSize> that takes the input length rather than uses null-terminated input (it does not read past the end of the buffer)
• manualVecStrlen_<StepSize> - function that first calls the standard strlen and then manualVecSize so it does not read past the end of the input buffer

The benchmarks were done for the following platforms:

1. amd-epyc - AMD EPYC 7282 @ 3.2GHz with 188GB of RAM (physical server)
2. intel-icelake-aws - Intel Xeon Platinum 8375C (Icelake server) CPU @ 2.90GHz with 252GB of RAM (m6i.metal AWS instance)

For both platforms code was compiled with GCC version 10.3.0.

For AMD EPYC the code was compiled on the same machine with flags -std=c++20 -O3 -ffast-math -Wall -DNDEBUG -march=native -mtune=native -mno-avx256-split-unaligned-load.

For Intel Xeon the code was cross-compiled with the flags: -std=c++20 -O3 -ffast-math -Wall -DNDEBUG -march=native -mtune=native -march=icelake-server -mtune=icelake-server and the following architecture features:

Note that the code for Intel Xeon was compiled with AVX-512 instructions but without allowing compiler to use 512-bit registers (no -mprefer-vector-height=512 flag).

Benchmarks were run for two inputs:

1. wp.txt - War and Peace by Leo Tolstoy, 3.2 MiB
2. long.txt - wp.txt concatenated 100 times, 320 MiB

Benchmarks was run multiple time in a row for each algorithm and input combination: 10 runs of 10 passes per run for wp.txt and 0 runs of 1 pass per run long.txt. The best (max speed) result was choosen. Benchmarks were run pinned to an isolated core.

Null-terminated input

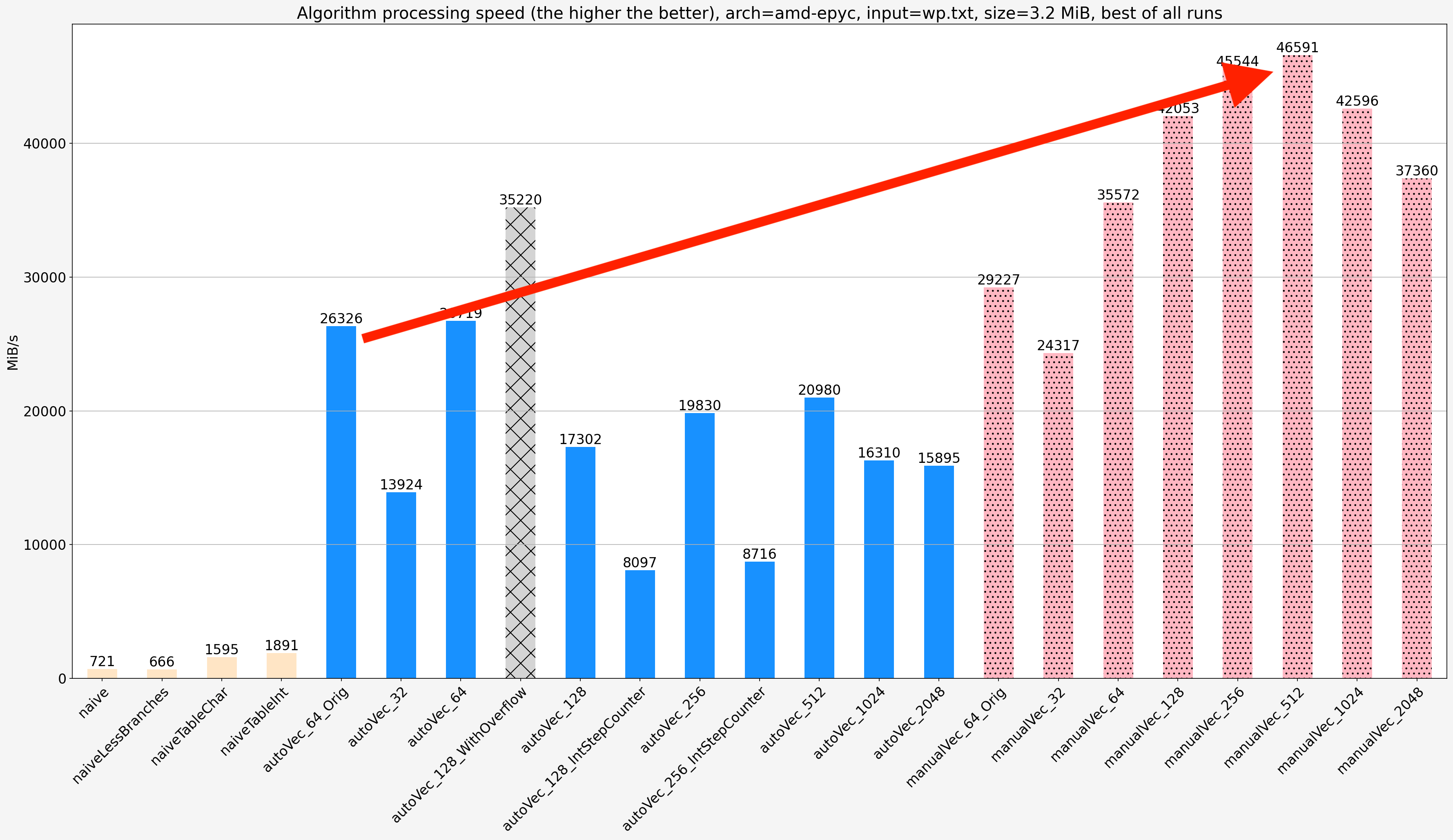
Small input (wp.txt, 3.2 MiB)

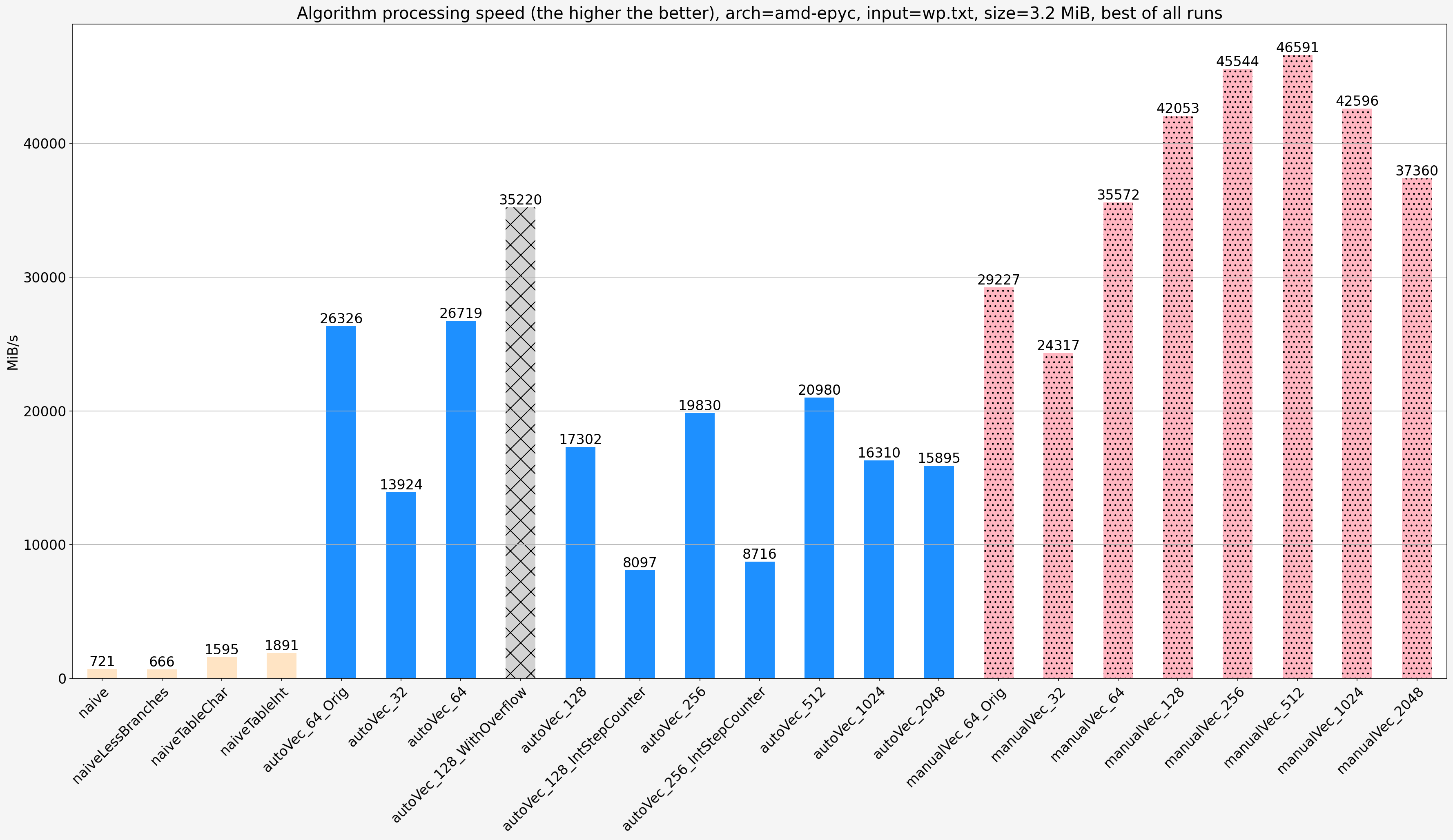
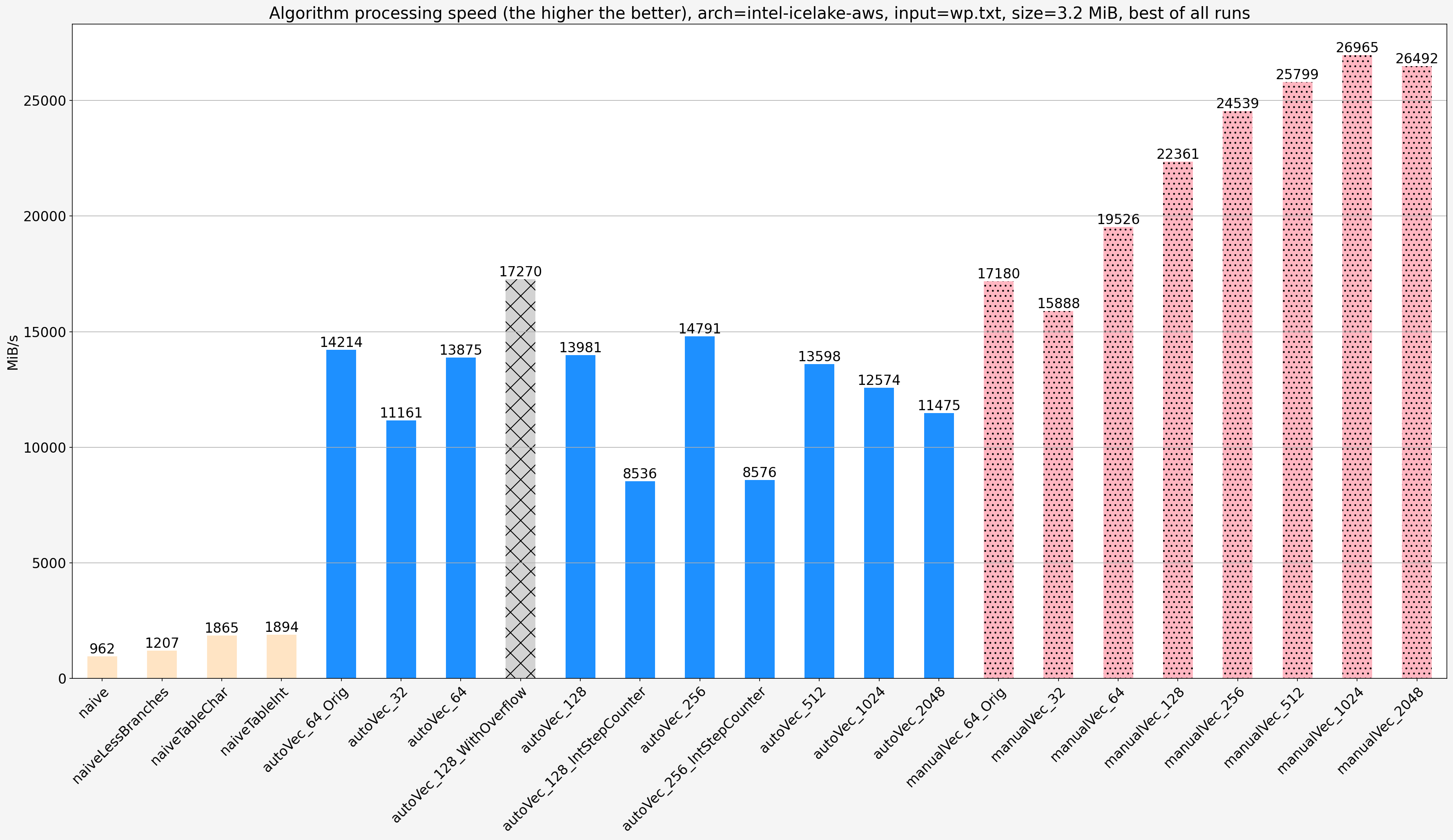
Notes:

1. The manually vectorized code is faster than the original auto-vectorized code (autoVec_64_Orig) by 1.35x-1.9x depending on platform and manually vectorized code step size.
2. Using short instead of signed char for step counter degrades speed by a factor of two on AMD platform, less on Intel platform
3. Using int instead of short for step counter degrades speed further by a factor of two on AMD platform, less on Intel platform
4. AMD EPYC and Intel Xeon show similar relative performance of different vectorized implementations. AMD platform shows better absolute proformance which can be explained by the fact that Intel platform is an AWS instance with worse RAM setup.

Large input (long.txt, 320 MiB)

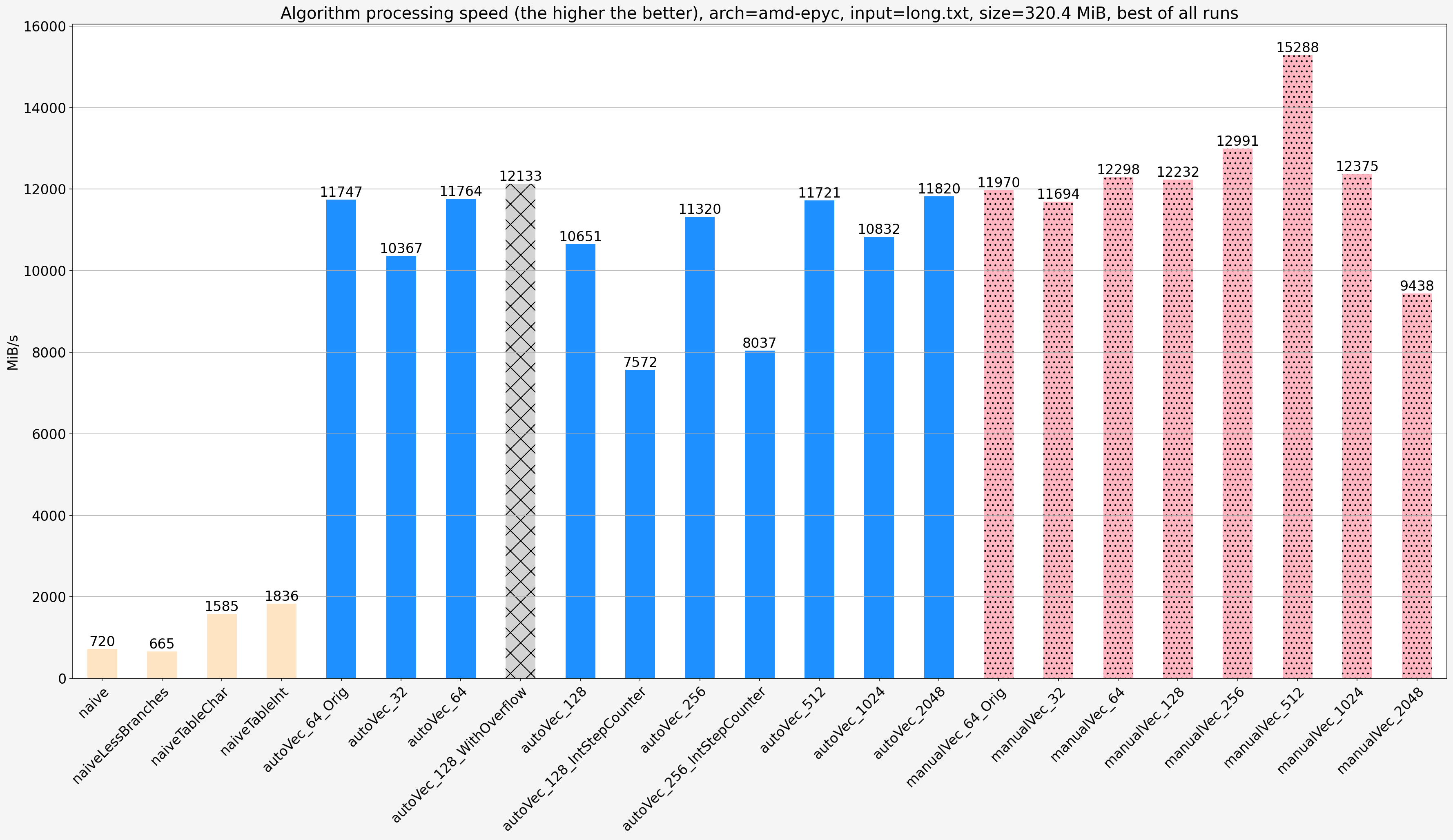
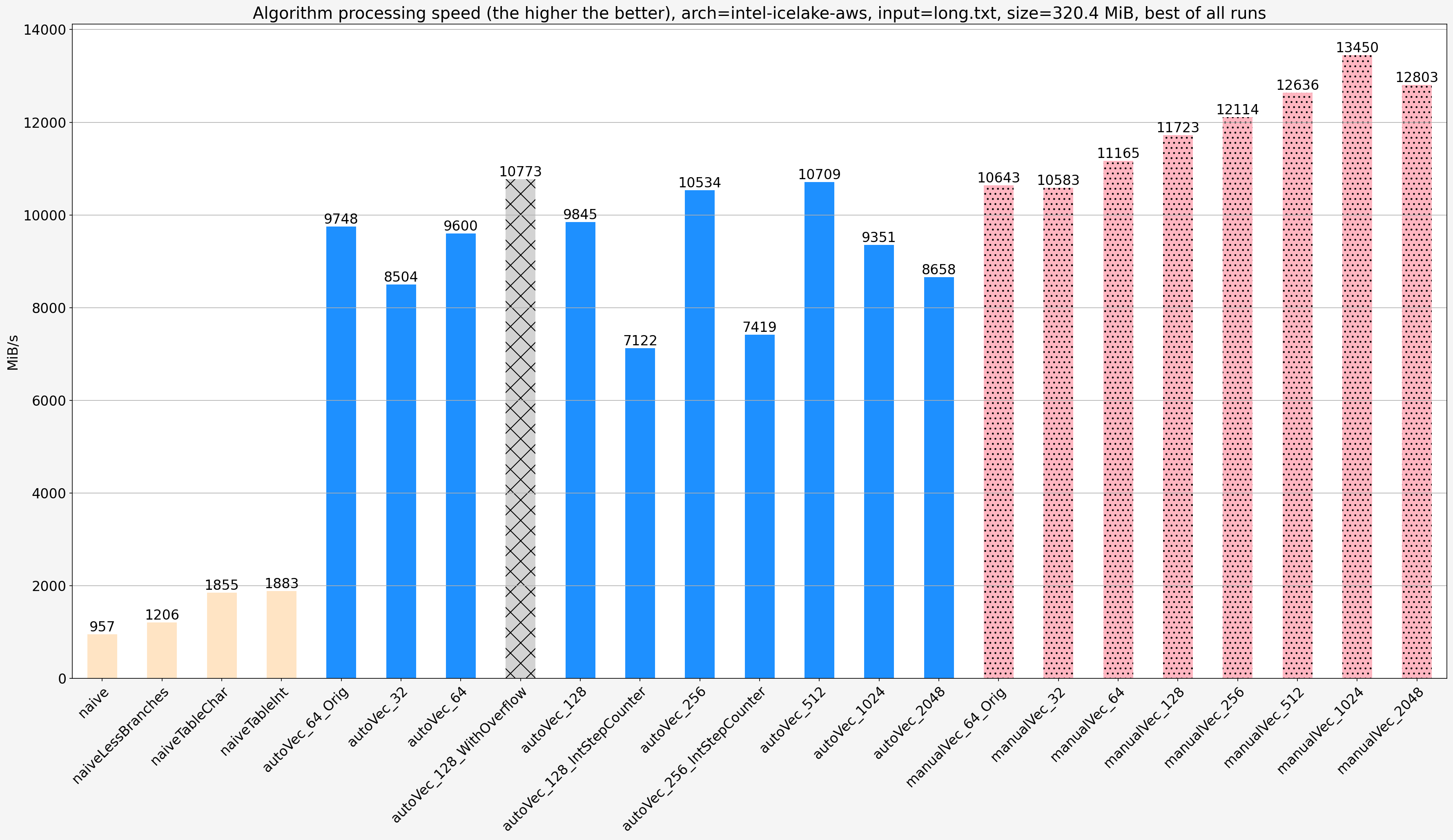
Notes:

1. When the input size is bigger than the cache size then there is a significant slowdown for all vectorized algorithms and they show less diffference in speed. The’re still significantly faster than non-vectorized solutions
2. There is no slowdown for non-vectorized solutions

I’ve run toplev from pmu-tools on Intel Xeon for both inputs to find where is a performance bottleneck.

For the small input wp.txt for all step sizes the execution is bound on Backend_Bound.Core_Bound.Ports_Utilization.Ports_Utilized_2 and Backend_Bound.Core_Bound.Ports_Utilization.Ports_Utilized_3m which simply means that the core fully utilizes some execution ports while executing 2+ uops per cycle, or even simplier, it is CPU bound.

For the long input long.txt for manualVec_128 the execution is bound on Backend_Bound.Memory_Bound.L2_Bound which means L1 cache misses and for manualVec_1024 it is bound on Backend_Bound.Memory_Bound.DRAM_Bound.MEM_Bandwidth which simply means loading data from the main memory.

Known size input

Small input (wp.txt, 3.2 MiB)

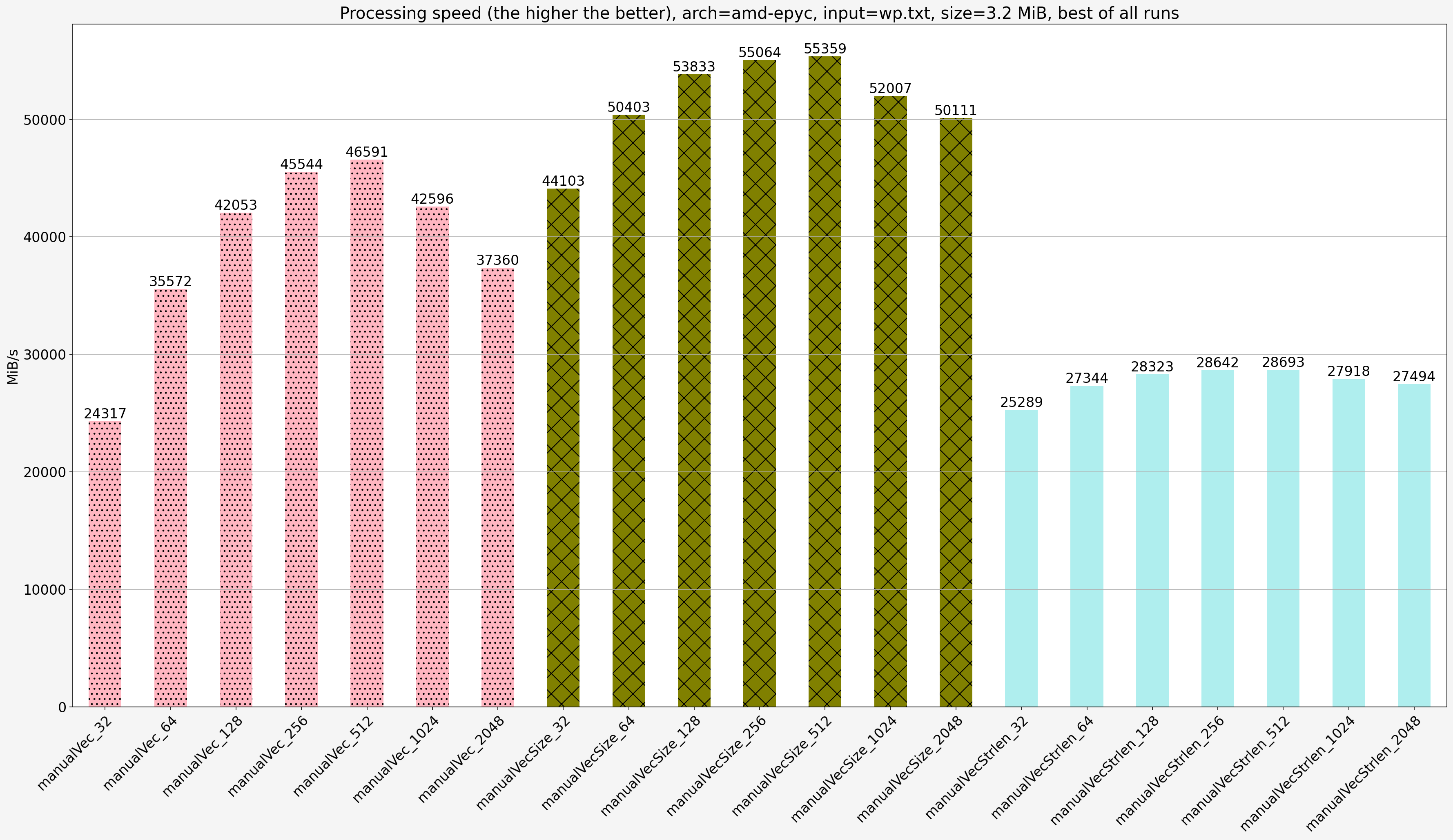
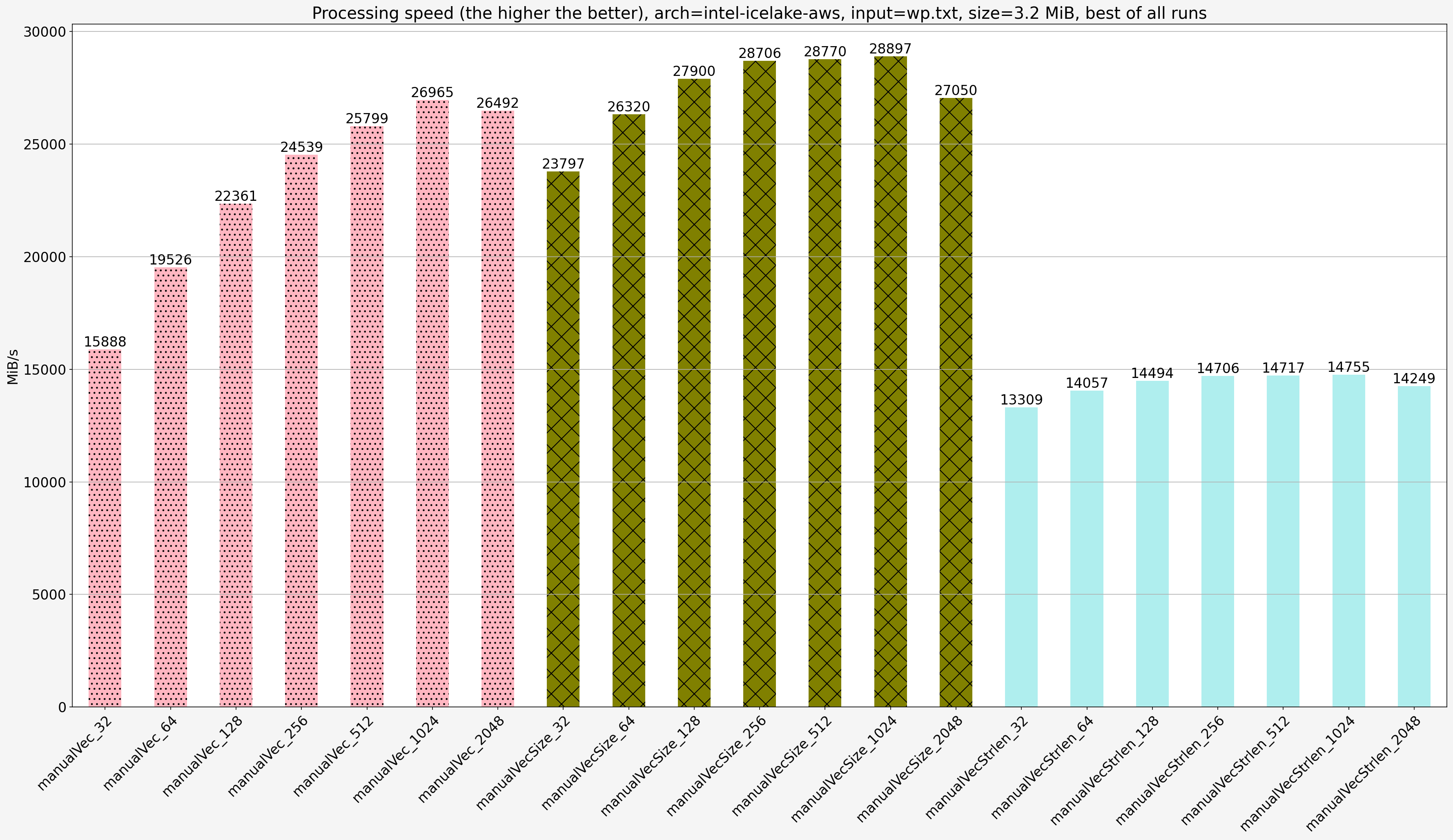
Notes:

1. For the same step size solution that takes the input size is faster than solution that relies on null-terminated input by 1.02x-1.81x
2. For the same step size manualVec is faster manualVecStrlen by 1.19x-1.86x except for step size 32 on AMD platform for which manualVecStrlen is faster than manualVec by 1.04x.

Large input (long.txt, 320 MiB)

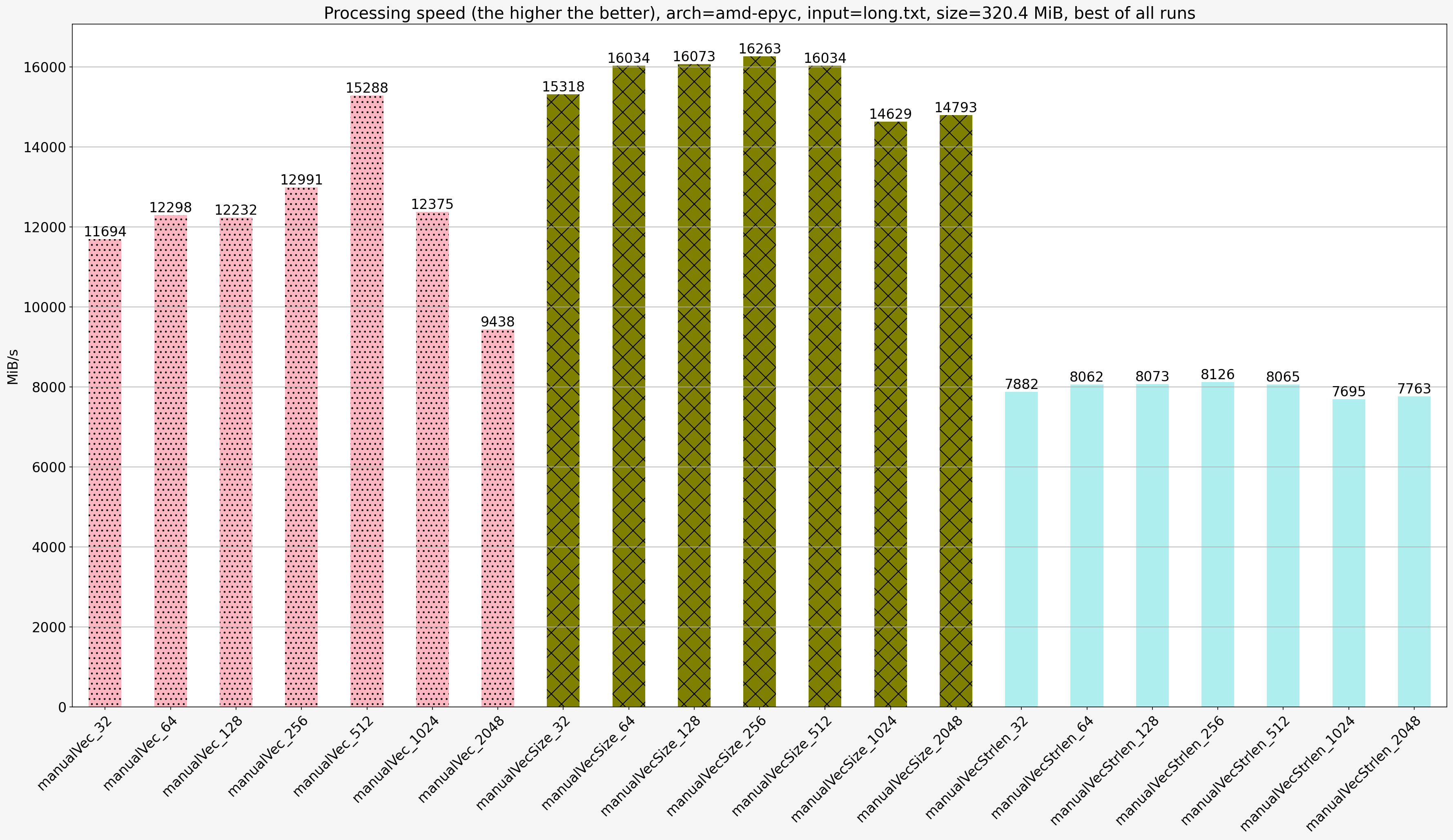
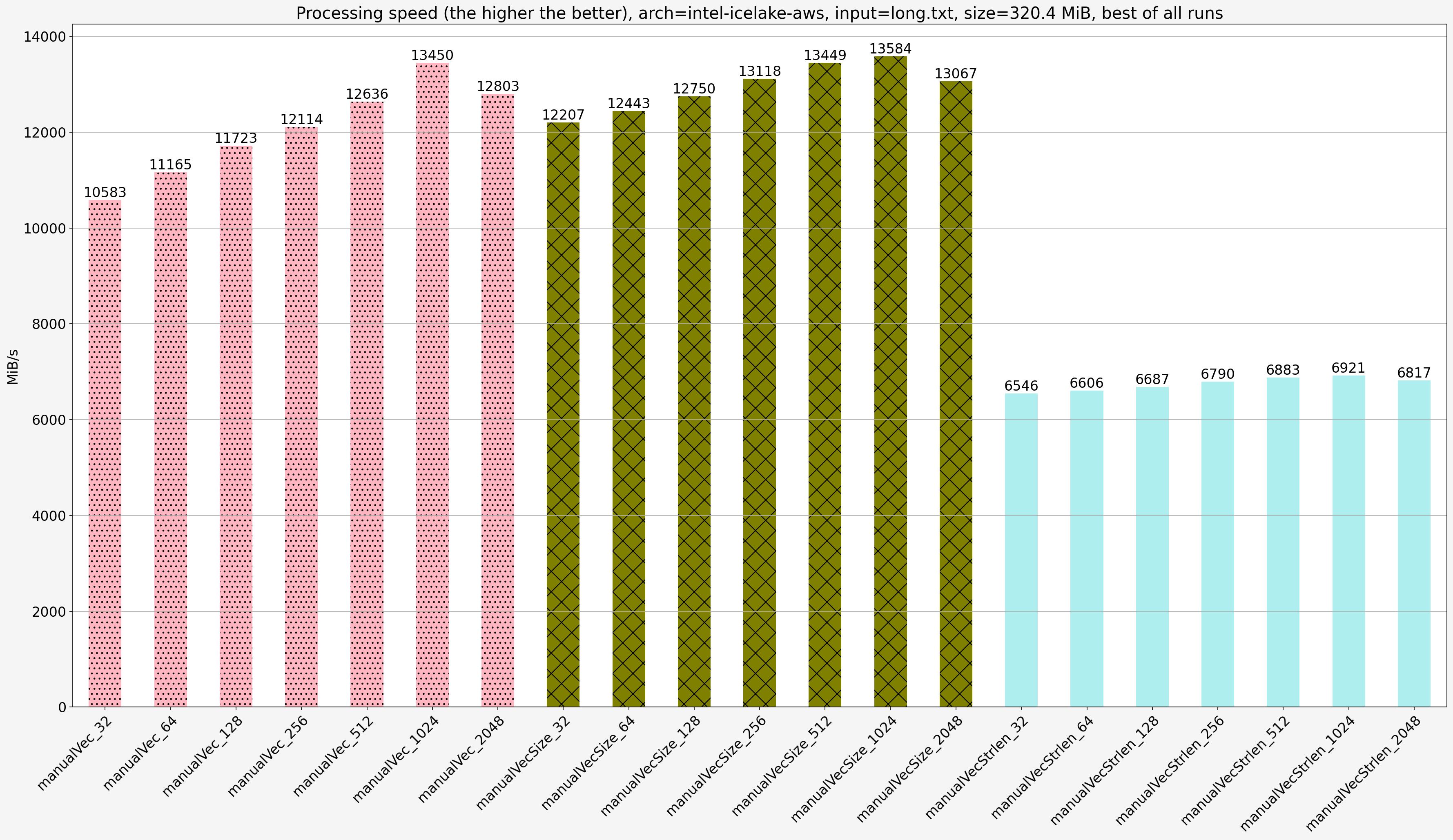
Notes:

1. Same as for the null-terminated input: when the input size is bigger than the cache size then there is a significant slowdown for all vectorized algorithms and they show less diffference in speed except for manualVecStrlen. The’re still significantly faster than non-vectorized solutions
2. manualVecStrlen become slower than manualVec on every step size

Conclusion

1. (Not surprizingly) the manually vectorized code is faster than the original auto-vectorized code (autoVec_64_Orig) by 1.35x-1.9x depending on platform and manually vectorized code step size.
2. When input is larger than the cache size then vectorized algorithms become bound by the RAM reading speed and show similar performance
3. Non-vectorized algorithms perform worse than vectorized ones by a factor of 10-60 when input fits into the cache and by a factor of 10-20 when input does not fit into the cache. Performance of this algorithms does not depend on the input size because they’re never bound by the RAM reading speed
4. In all but one scenarios better performance (by 1.19x-1.86x) was achieved if size of the input is known in advance. The implementation is also less complex in this case.
5. The best step size for my manually vectorized implementation is between 256 and 1024
6. AMD EPYC and Intel Xeon show similar relative performance of different implementations. AMD platform shows better absolute proformance but this may be simply attributed to the fact that Intel machine is an AWS instance with unknown memory setup
7. GCC/C++ compilers are spectacularly creative with auto-vectorization
8. Auto-vectorization as many other types of compiler optimizations is fragile. E.g. innocently looking change of a variable type has decreased performance by a factor of 2
9. Using intrinsics instead of assembler is handy. It allows to concentrate on algorithm vectorization itself and delegate to the compiler the low-level machinery like register assignment and (hopefully optimal) instruction reordering

Future work

1. Analyzing auto-vectorized code when 512-bit auto-vectorization is enabled (-mprefer-vector-height=512 and AVX-512 feature flags)
2. Manual optimization with using AVX-512 instruction set
3. Force compiler to produce auto-vectorized code performing as the manually optimized one without using intrinsic functions or assembler
4. Run AMD μProf to find bottlenecks on AMD CPU to conclude the bottleneck findings for Intel CPU
5. Getting benchmark results for other compilers, CPUs and even platforms. Optimizing for Apple ARM-based CPUs would be particularly interesting.

Links

1. Code and benchmark results on GitHub
2. Intel Intrinsics Guide
3. x64 Cheat Sheet and x86-64 Assembly Language Summary - assembler refreshers
4. x86 and amd64 instruction reference
5. Latency table and another one
6. Agner Fog’s manuals on low level software optimization, contains a latency table and a lot of useful links
7. Denis Bakhvalov Top-Down performance analysis methodology - an introduction into Top-down Microarchitecture Analysis Method (TMAM)
8. Intel 64 and IA-32 Architectures Optimization Reference Manual

Software performance analyzers:

1. pmu-tools - an easy to use performance analyzer for Intel CPUs
2. AMD μProf (uProf, “MICRO-prof”) - AMD’s official profiler for AMD CPUs
3. Intel VTune Profiler - Intel’s official profiler for Intel CPUs

Updates:

2023-08-07:

• Fixed typos
• Fixed errors in relative performance numbers
• Rephrased notes for benchmark results

2023-08-08:

• Added comments to asm diagrams